感度と有病率をplotする自作関数をRで実装(ブログ上でコード動かせます)
感度と特異度を把握している状態で,検査人数と陽性者数が分かれば,背後の真の有病率を推定することができることは,前に説明(←有病率の推定方法.数式が多いので,興味ある人だけどうぞ!)しました.
# 陽性率≠有病率
もちろん感度が変わると背後の真の有病率も変化するのですが,どのような範囲で有病率が推移するのかについて,前回の数式の関係性をもとに自作関数を作成しました.
# 自作関数はfunction(変数){関係式}で作成することができます.
下のコードで▶︎を押すと,結果が出力されます.
万が一,うまく実装されなかった人がいた場合のために結果の図を下に載せながら,コードなどの説明をしていきます.
なお図では黒色が点推定値,青色が区間推定(95%信頼区間)になります.
# 特異度99%, 陽性者数100人,合計の検査人数800人の場合
R上で自作関数f()を定義したあとで,f(0.99,100,800)と打てばよく,
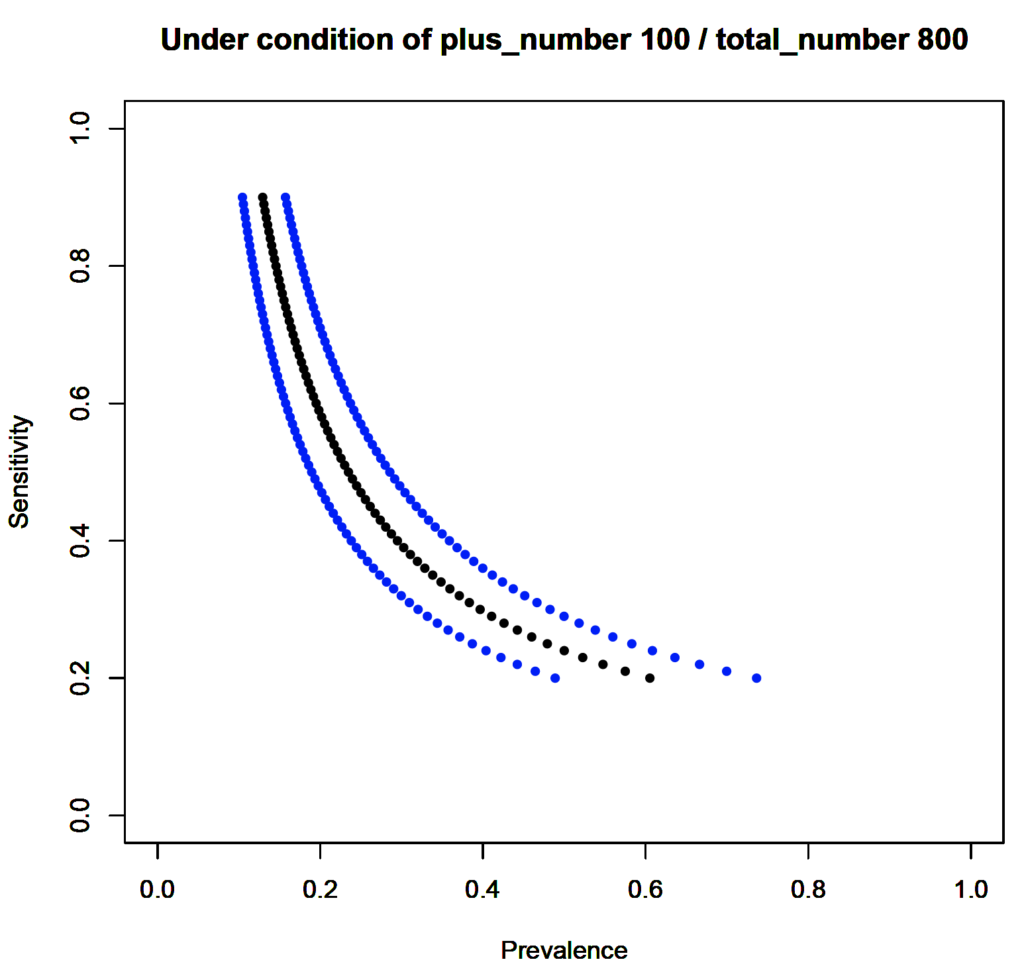
図のように,感度が下がれば,それに応じて有病率の推定値が上がってくことが確認できました.もとの検査陽性率が12.5%なので,感度が50%以下のところでは,有病率と検査陽性率の隔たりが大きくなる印象でしょうか.
# 特異度99%, 陽性者数4人,合計の検査人数67人の場合
こちらもf(0.99,4,67)と打ってあげればよく,
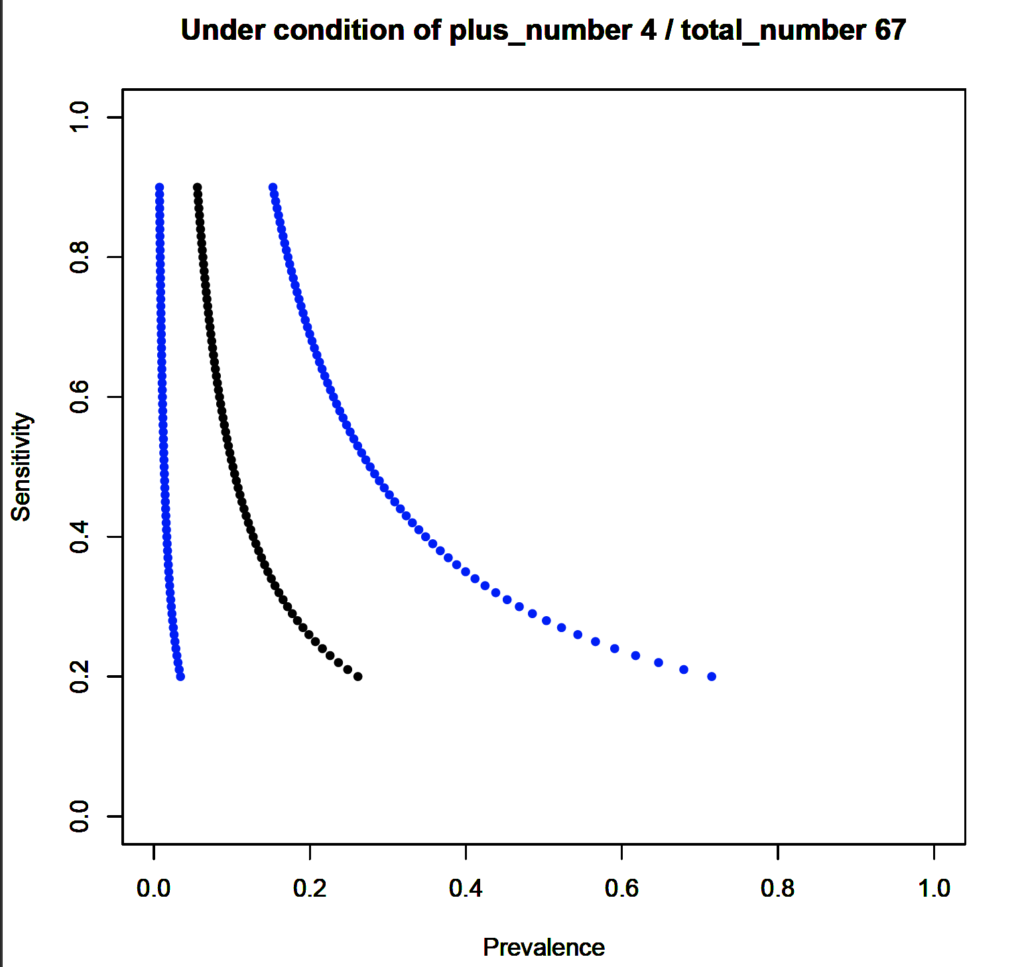
そもそもの検査人数が少ないと有病率の信頼区間が大きくなってしまいますね.
感度60%以下ではとくに信頼区間が大きくなってしまっている印象です.
どこかの時点で,有病率をきっちり調べるために,サンプルサイズ計算をすることになった場合,検査の感度がある程度きまっていないとサンプルサイズ計算が大変な作業になるような気がしました.(あくまでも個人的な感想です)
上に載せてあるコードは,いろいろいじることが出来ます.よかったら数値を色々変えながら検討してみてくださいね〜
今日はこの辺で!
(参考リンク)
そもそも感度・特異度とは?(感度と特異度の臨床的解釈のページに飛びます.)