医学統計入門③ 統計的有意≠臨床的有意
前回の検定の復習
前回の入門②では仮説検定のあらましについて話しました
- 帰無仮説 H0 が成立している仮定の下で論理展開して
手元のデータがH0 由来の可能性が低い(P < 0.05)なら
H0 を否定して対立仮説 H1 を採択,つまり統計的有意差あり!
という流れでした
統計的有意≠臨床的有意
検定は「有意 / 有意でない」の二元論的に(非対称な)意思決定をするツールでしたが
検定の中で差の程度を言及してもらえるわけではないので
小さな差しかない場合,臨床的に有意であるとはいえないのです.
つまり有意差が得られても,臨床で使えるのかは全く別問題です.
具体的には,研究データの人数を超大量に集めると,仮説検定の精度が良くなり,
「尿路感染症の治療効果が1%だけ良くなる新薬」や「HbA1cを0.1だけ下げる高額な新薬」も有意差あり!と判定されてしまいます
大規模な研究だと,患者の特性を並べたTable 1で二つのグループの年齢がほぼ一緒なのにP < 0.05になっていたりすることがあります.
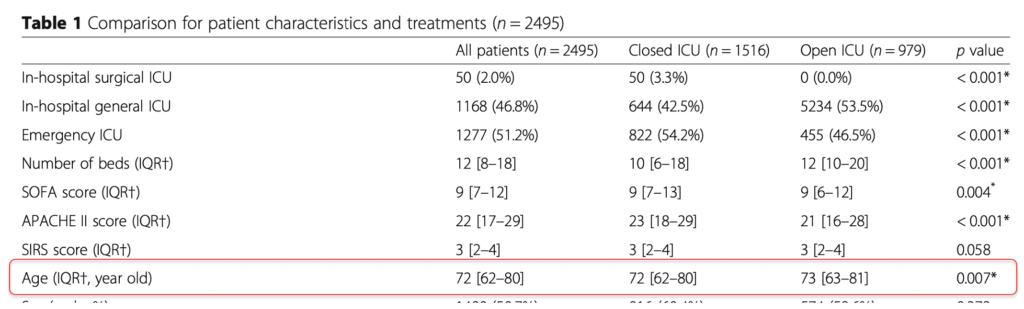
Closed ICUのグループの中央値が72歳,Open ICUのグループでは73歳で,たしかに統計的には有意な差(P=0.007)があるのですが,
「臨床的には,そんな差は意味がない」ですよね…
検定統計量でナゾを紐解く
なぜ統計的有意≠臨床的有意になっているのか検定統計量を注目することで明らかになります
簡単な数式で見ていきましょう
検定統計量は以下の式で定義されます

数式中の「観測値 − 期待値」が臨床的な差です
例えば,血圧降下の差があるかの検定をするときに,
データ上の平均値(=観測値)で10下がったとします
一方で帰無仮説H0の仮定の元での期待値は0(ゼロ)です.
この時,観測値と期待値の差は10になり,これが臨床的な差に相当します
ただ,この臨床的な差は,血圧や身長や尿量などによって大きさが逐一変わってきます
それを標準誤差という“ばらつき具合”によって,調整したものが検定統計量です
検定統計量は統計的な差に相当し,一定の閾値を超えると「有意」,超えなければ「有意でない」と判定します
ここでNがとても大きい場合を考えてみましょう

Nが増えると,標準誤差が小さくなり,推定精度が良くなっていきます
臨床的な差が小さくても,検定統計量は閾値を超えた場合に統計的有意差が得られてしまうのです
- 統計的有意と臨床的有意は異なる概念なので
P<0.05でも臨床的に意味があるのか考えるのはとても大切です! - この臨床的な差のことを統計の本では効果サイズと呼んだりします
- 標準誤差についてもっと知りたい場合はリンクなどを見てください
検定統計量と検定の種類
いままで総論的に検定を見てきましたが,世の中にはたくさん検定がありますよね
実は,変数の型(カテゴリカル,連続),グループ(標本)の数によって検定統計量の性質が変わってきます
きちんと言うと,変数や標本に応じて検定統計量が従う分布が変わってきます
2値変数ならカイ二乗分布に従いますし (カイ二乗検定)
連続変数なら(t分布など)に従います (t検定)
近似させる分布の数だけ検定の種類がある,ということです
よく使われる検定の一覧表はこちら↓です
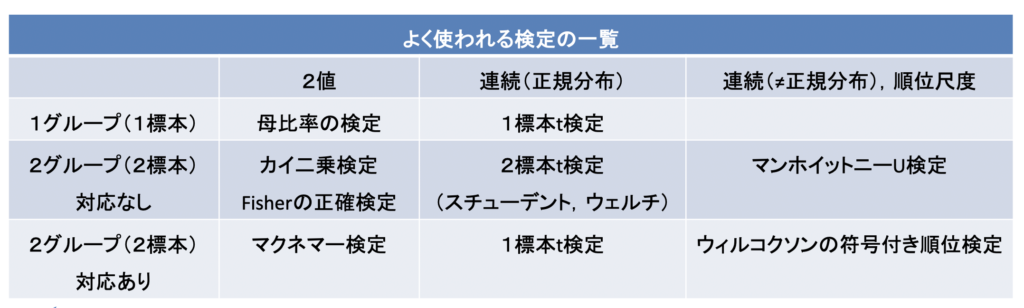
統計そのものを数学的に研究する場合は,t検定の細かな数式の導出などを勉強する必要がありますが,医学研究で用いる統計では,そのような細かなことまでは使いません
それよりも大切なことは
- 総論的に検定の本質を理解し,正しく解釈でき,
- 研究のデザインに応じて適切な検定を用いる,ことです
おまけ:いやいやt検定の導出も全部知りたいという人は,ちゃんと逃げずに説明しているブログや動画をみてみるといいかもしれません.ただすごく長くなるので,気合いを入れて見る必要があるかもです
まとめ
統計的有意と臨床的有意は異なる概念であることから出発し,
検定統計量を通じて両者の関係を勉強しました
また,この検定統計量の性質が研究デザインによって変わるため,
検定にはたくさんの種類がある,と知ることができました
次回(入門④)は,検定統計量のところで出てきた臨床的な差(効果サイズ)の指標を用いて,βエラーや検出力の概念を見ていくことにしましょう
βエラーや検出力の概念を理解できると,サンプルサイズ設計(研究の適切な標本数N)も理解できるようになります
ここまで読んでいただき,ありがとうございました!
