Firthの方法と自作関数
#Firthの方法はややマニアックな領域です.ある程度,統計の知識があるのを前提に記事を作成しています.
ロジスティック回帰でモデルが準完全分離しているとき,尤度関数は非常に大きくなり,パラメータ,つまりオッズ比の推定が非常に不安定になります.
なかなかデータが集まりにくい分野では,症例数100を集めるのも難しい領域があり,ときどき完全分離に関する統計相談を受けることがあります.難しい問題ですよね.
完全分離しているときは対応方法はいくつかあると言われていますが,
1 説明可能なサブ集団に対して,準完全分離をロジスティック回帰を行う
2 Firthの方法を使って,尤度関数に罰則をつける.(準完全分離の場合)
3 Exact logistic regressionを試みる.(準完全分離の場合)
などが代表的でしょうか.
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
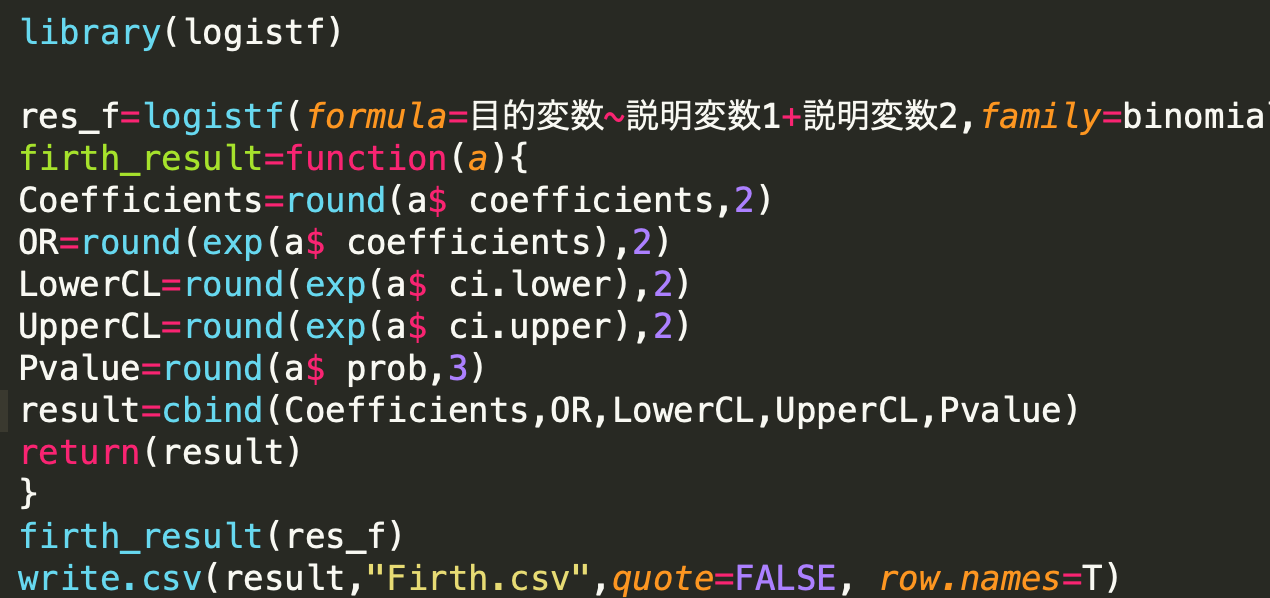
# ライブラリの読み込み library(logistf) # firth logistic regression model の作成 res_f=logistf(formula=目的変数~説明変数1+説明変数2,family=binomial,data=df,firth=TRUE) # モデルの要約した表を作る関数を作成 firth_result=function(a){ Coefficients=round(a$ coefficients,2) OR=round(exp(a$ coefficients),2) LowerCL=round(exp(a$ ci.lower),2) UpperCL=round(exp(a$ ci.upper),2) Pvalue=round(a$ prob,3) result=cbind(Coefficients,OR,LowerCL,UpperCL,Pvalue) return(result) } # 作成した関数を使って先ほどのモデルに投入 firth_result(res_f) # 結果をCSVファイルに書き出す write.csv(firth_result(res_f),"Firth.csv",quote=FALSE, row.names=T) |
ソースコードでコピペできない場合は↓のコードで試してみてくださいm(_ _)m
library(logistf)
res_f=logistf(formula=目的変数~説明変数+説明変数1, family=binomial, data=df, firth=TRUE)
firth_result=function(a){
Coefficients=round(a$ coefficients,2)
OR=round(exp(a$ coefficients),2)
LowerCL=round(exp(a$ ci.lower),2)
UpperCL=round(exp(a$ ci.upper),2)
Pvalue=round(a$ prob,3)
result=cbind(Coefficients,OR,LowerCL,UpperCL,Pvalue)
return(result)
}
firth_result(res_f)
write.csv(firth_result(res_f),”Firth.csv”,quote=FALSE, row.names=T)
コードの説明
library(logistf)でパッケージを立ち上げます.初めて使うときは,
install.packages(“logistf”)を打ってダウンロードしておきましょう.
次のlogistf()がモデル式です.モデル式の名前をres_fとしました.
その次からが自作関数firth_result()です.モデル式をテーブル形式で変換,出力させてあげる関数です.
最後に,write.csv()でファイルの書き込みが完了します.
説明終わり.
Firthの方法の説明として,一応参考サイトも載せておきます.実用重視の人は一番最後の日本語のサイトで十分かもしれないです.
パッケージlogistfのサイト
https://cemsiis.meduniwien.ac.at/kb/wf/software/statistische-software/fllogistf/
完全分離と準完全分離についての英語のwikipedia
https://en.wikipedia.org/wiki/Separation_(statistics)
RのFirthの使い方の説明をしている他のサイト