医学統計入門② 仮説検定は背理法に似ている
前回,医学統計入門①で「なぜ医学研究で統計が必要になるのか」について話しました
この記事では統計的推測で頻用される仮説検定について,わかりやすく解説します
- 注:この記事は少し長くなってしまいました….読むのが辛くなった場合,最後のまとめを読んで理解を深めたい箇所を辿ってもらう方がいいかもしれません
目次
仮説検定の例
仮説検定は色んな場面に出現します.例えば,
- 血清コレステロールは男女間に差があるか
- 頭痛に関する2つの治療方法の比較
- 朝型・夜型生活と心疾患の発症の比較
などです
仮説検定の手順(背理法に似ている)
下準備:帰無仮説(H0)と対立仮説(H1)
まず下記のように2つの仮説を用意します
- 帰無仮説(H0) : 差がない,効果がない
- 対立仮説(H1) : 差がある,効果がある
具体例ですと
- 帰無仮説(H0) : LDLコレステロールは男女間に差がない
- 対立仮説(H1) : LDLコレステロールは男女間に差がある
などになります
帰無仮説(H0)のもとで論理を展開
仮定の下での標本の平均の分布を考える
まず,帰無仮説H0が正しいと仮定します
このとき,例えば男性100人と女性100人のLDLのデータ(標本)を集めたら
「男性のLDL平均値 − 女性のLDL平均値」
はゼロに近い値をとるはずです
ただ,毎回ゼロになるわけではなく
当然データのばらつきがあるはずなので
下図のようなゼロを中心とする分布に基づいた値をとることになります
実際に得られたデータの値との比較
ここで例えば,実際のデータで得られた値が2.17だったとしましょう
つまり,下の図では緑の矢印の位置になります
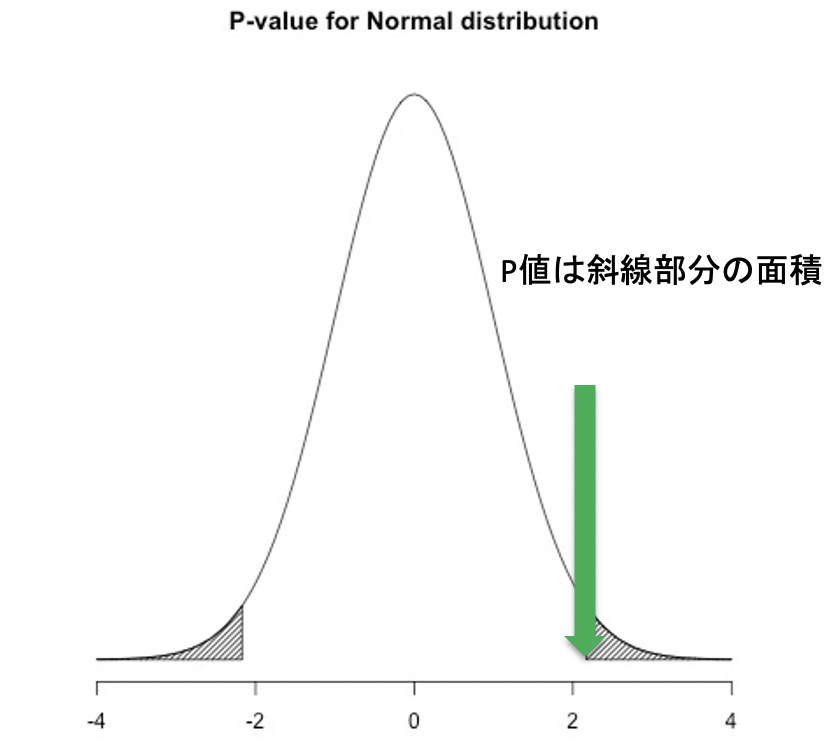
この緑の矢印の位置か,あるいはさらに極端に差があるデータが得られる確率(=P値)を評価します
ちなみに上の図だと,P=0.03です
帰無仮説の仮定のもとでは,
3%しかない”非常に珍しい”データが得られたということになります
帰無仮説H0が成立しにくい→対立仮説H1採択
帰無仮説の仮定のもとで3%しか起き得ない”非常に珍しい”データだったと考えるか,そもそも仮定が間違っていたと考えるのか,とても悩ましいですね
そこで判定基準をつくるために,
データのばらつきの許容範囲内と考えるべきか,
そもそも仮定が間違っていると考えるべきか
有意水準を設けることにしましょう.
多くの場合,慣例として有意水準を0.05と設定している場合が多いです
- P値が有意水準(0.05)より小さければ「有意差あり」と判断
- 仮定(H0)が成立しているという主張を棄却して,対立仮説H1を採択する
- P値が有意水準(0.05)より大きければH0の仮定は棄却しない
cf. 背理法の手順 \( \sqrt2\)が無理数であることの証明
仮説検定は独特なアルゴリズムに沿って実行されますが,実は背理法と似ています
復習がてら,背理法の例を見てみましょう
下準備:帰無仮説(H0)と対立仮説(H1)
下記のように2つの仮説を用意します
ふだん背理法では帰無仮説,対立仮説という用語はあまり使いませんが,
対比するために,ここでは敢えて使うことにします
- 帰無仮説(H0) : \( \sqrt2\)は有理数である
- 対立仮説(H1) : \( \sqrt2\)は無理数である
帰無仮説(H0)のもとで論理を展開
「H0: \( \sqrt2\)が有理数」と仮定
このとき, \( \sqrt2 = \frac{p}{q}\) と表すことができる(\( \frac{p}{q}\)は既約分数)
変形すると,\(\mathrm{2q}^{2}=\mathrm{p}^{2}\)となるので,pは2の倍数
このとき, \(\mathrm{p}^{2}\)は4の倍数になるので,\(\mathrm{q}^{2}\)も2の倍数. つまりqも2の倍数
よってpもqも2で割り切れてしまうが,
これは既約分数であることに反する(H0は矛盾)
帰無仮説H0が成立しない→対立仮説H1採択
H0が成立している仮定のもとで,論理展開してみたところ,矛盾が生じてしまいました.
よって,仮定(H0)が成立しているという主張を棄却して,
H1を採択,つまり,\( \sqrt2\)は無理数であることが分かりました
仮説検定と背理法の共通点,相違点
両方の共通点と相違点を見ていきましょう
- 2つの仮説(H0, H1)を用意
- H0が成立している仮定の下,論理展開
- H0を完全否定するのが背理法,H0の可能性が低いことを指摘するのが仮説検定
- H0を否定→H1を採択
と,仮説検定と背理法の流れは同じで,三番目以外は共通していることが分かりました
仮説検定の非対称性
ここまで明記していませんでしたが,P > 0.05となったときの解釈は重要です
- P < 0.05 → 有意差あり!
- P > 0.05 →
差がない→ 差があるともないとも言えない(無に帰す)
P値が有意水準(0.05)より大きい場合,帰無仮説H0を棄却することはできません
とは言え,H0が真であることを積極的に信じるということはせず,
捨てるのに充分な証拠がない,つまり判定を保留します
まさしく「棄却されなければ,無に帰す仮説」というわけで
帰無仮説と命名した人は相当センスがあったと思います
まとめ
長文でしたので,仮説検定の要点をまとめます
- 2つの仮説(帰無仮説 H0, 対立仮説 H1)を用意する
- H0 が成立している仮定の下,論理展開する
- 手元のデータがH0 由来の可能性が低い(P < 0.05)なら,H0 を否定→H1を採択
- 手元のデータがH0 由来の可能性が低くない(P > 0.05)なら,判定を保留する
- 仮説検定の手順を忘れそうになったときは背理法で思い出す
わからないところがあれば遡って読んでもらえたらと思います
実は仮説検定で有意差が得られても,臨床的に殆ど意味がない場合があります.
次回,医学統計入門③で詳しく見ていくことにしましょう!
