医学統計入門⑤ 推定
前回,無事に検定が終わったので,今回は統計的推測のもう一つの柱である推定について見ていくことにしましょう
はじめに:推定は統計的推測の一つ
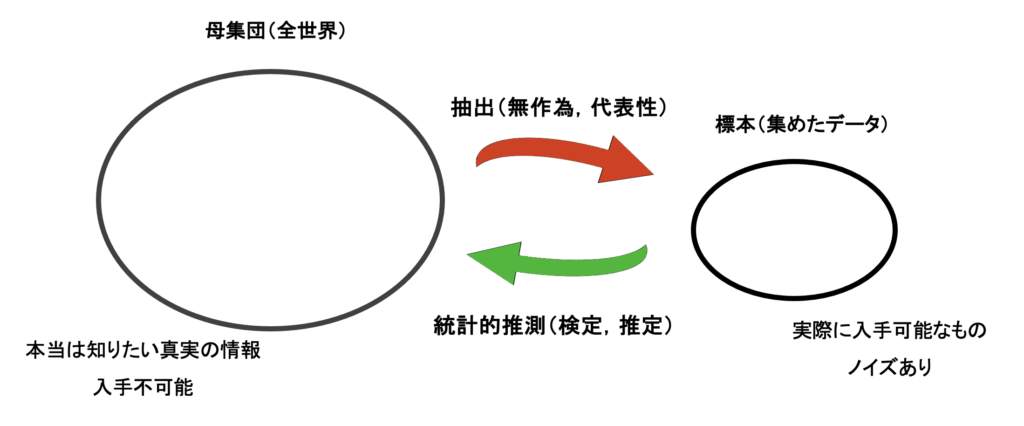
検定は手元のデータ(標本)をもとに母集団に対して「H0: 差がない」vs「H1: 差がある」の意思決定をするものでした.しかし,差があるだけでは情報不足で,どれくらいの差があるのかを知りたい場面も多いと思います.
- 例1 枕の効果
新しい枕を買った時に,入眠までの時間が短くなるか(=枕の効果)を調べたいとしましょう.検定により入眠までの時間が有意に短くなるのが分かっても1分の差なのか30分の差なのか,わかりません.
10人のデータを集めたところ,入眠までの時間が平均として20分短くなったとしましょう.この情報をもとに,母集団に対して枕の効果は何分と推定するのが妥当でしょうか.またその推定の信頼性も気になります.
点推定と区間推定
具体的な数値がどのようになるかを検討するのが推定です.上記の枕の例だと手元のデータの平均が20分なので,母集団に対する推定も20分とするのが妥当でしょう.
このように母集団の平均などを一つの値で推定する方法を点推定と呼びます.
さらにこの点推定の信頼性を考えてみましょう.バラツキ具合とデータの数によって信頼性は変わってきます.平均20分といっても,「全員が20分の場合」と「5分だったり60分だったりがバラバラの中での平均20分の場合」だと前者の方が信頼性が高まります.また高々10人のデータより100人や1000人のデータの方が信頼できるでしょう.
この点推定の信頼性,裏返すと点推定の不確実性を区間で表したものが区間推定になります.医学研究では特に95%信頼区間が用いられることが多いです.
平均\( \overline{X}\),バラツキ具合を標準偏差σ,データの数をNとして,これを数式で書くと
- 点推定値: \( \overline{X}\)
- 95%信頼区間:\( \overline{X}-1.96×(σ/\sqrt{N})\) 〜 \( \overline{X}+1.96×(σ/\sqrt{N})\)
のように計算することができます(数式を暗記する必要はありません)
データ数と信頼区間:数式を紐解く
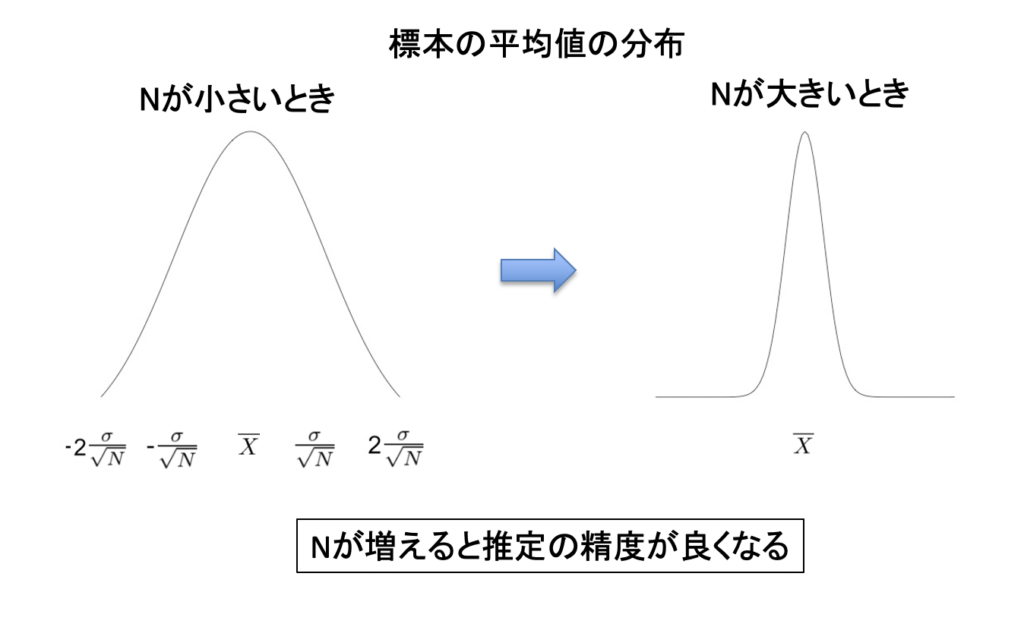
数式を見てみるとNが小さいとき,平均値(\( \overline{X}\))の95%信頼区間が大きくなり,推定の精度は悪いです.
Nを増やすと,平均値(\( \overline{X}\))の95%信頼区間が小さくなり,推定の精度が良くなります.
具体例での検討
概念ばかり話していてもわかりにくいと思うので,実際に計算してみましょう!
- 例2 糖尿病患者の血圧について
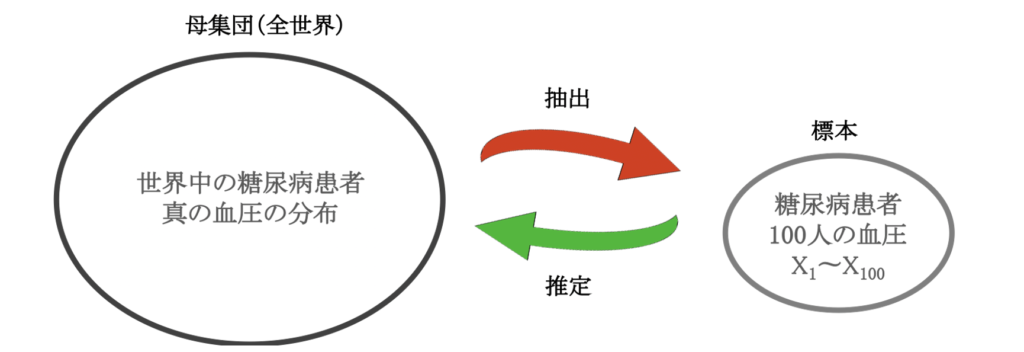
40代男性の中で2型糖尿病(DM)と診断された人の収縮期血圧の分布を知りたいとする.健常の40代男性の収縮期血圧の平均を130としよう.100人分(=N)のデータを収集したところ,データの平均値\(\overline{X}\)は135mmHg, (不偏)標準偏差(≒σ)は20であった.
このデータをもとに,一般的なDM患者の収縮期血圧の推定値,および95%信頼区間を求めたい.
N=100,\(\overline{X}\)=135, σ =20として点推定値と95%信頼区間を計算すればよく
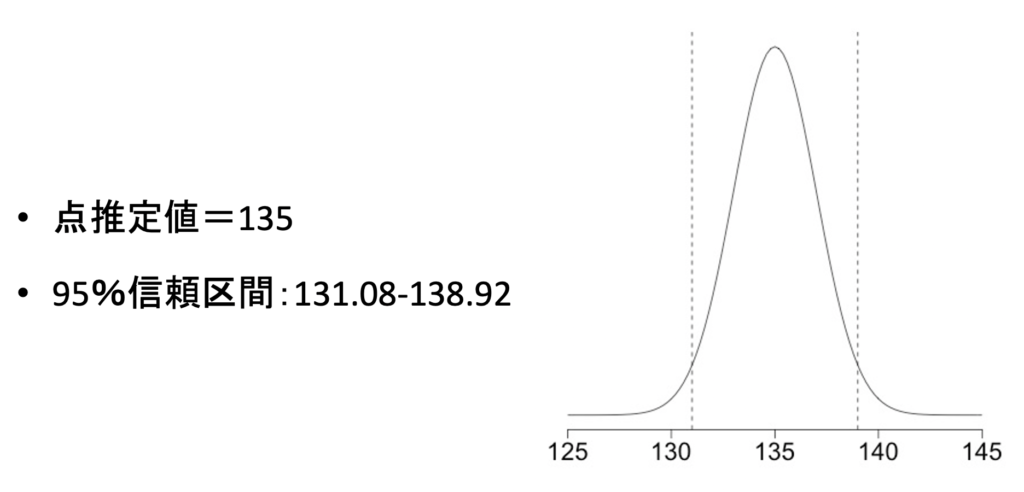
となり,手元の100人のデータを用いることで,40代男性の糖尿病患者の母集団における収縮期血圧の平均は131-139あたりにあるのだろうと推定することができました.
検定か推定か
検定は意思決定をするのに有用な手法です.
しかし検定だけですと,他の解釈が犠牲になってしまいます.研究の結果を1つのP値だけで表した場合,差の程度を知ることができません.
差の程度も重要なので,適切な推定値と信頼区間を提示する必要があります.統計的推測では検定だけでなく,推定も合わせて考えると良いでしょう.
信頼区間とP値の対応関係
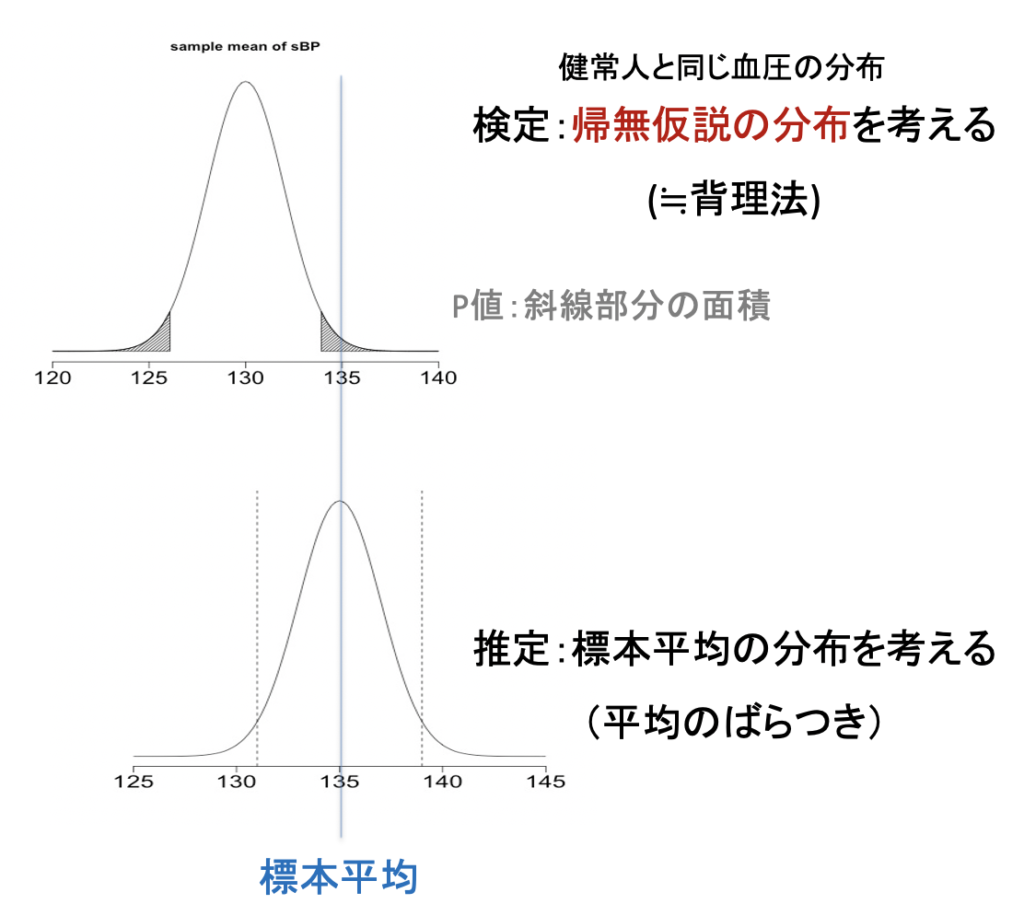
下の図のように95%信頼区間の外で帰無仮説の値を設定すると,P値は0.05より小さくなります.
検定では帰無仮説,つまり差がないと仮定したもとで得られるであろう平均値の分布を考えるのに対して,推定は手元のデータ(標本)の平均値の分布を考えています.
まとめ
- 手元のデータから母集団に対して統計的推測をしたい
- 統計的推測には検定と推定がある
- 検定は差の有無の意思決定ツール
- 推定では差の数値を点推定で,確信の程度を区間推定で求める
- 医学研究では区間推定として95%信頼区間が頻用される
- Nを増やすと95%信頼区間の幅が小さくなり,推定の精度が上がる
- 信頼区間とP値は対応関係がある
次回からは回帰のお話をしていきます.XからYを予測(ex. 身長から体重を予測)するときに回帰は重要なツールになります.回帰まで理解できると医学統計の見通しがかなり良くなります.
(おまけ)95%信頼区間は頻度論的立場からより厳密な解釈が為されることもありますが,有益性があまりないので割愛しました→詳しい説明はリンクなど
