医学統計入門④ 検定におけるサンプルサイズ設計
目次
はじめに
今回が仮説検定のお話の最終回になります.P > 0.05のときの解釈を深めつつ,サンプルサイズ設計のお話まで進めることにしましょう
入門②の検定のあらましで,仮説検定の解釈の非対称性について述べました.
- P < 0.05 → 有意差あり!
- P > 0.05 →
差がない→ 差があるともないとも言えない(無に帰す)
P > 0.05では「H0: 差がない / H1: 差がある」の判定を保留するということでしたが,一定の条件下で
- P > 0.05 → 差がない
に近い解釈することが可能になります!
この一定の条件下というのが実は大事です
具体例で仮説検定の概要を復習しつつ,見ていくことにしましょう
仮説検定の具体例
コインAがあるとします.このコインAはイカサマかもしれず,表が出る確率が通常のコインと比べて違うかどうか知りたいとしましょう.ここで実際にコインAを20回投げて7回,表が出ました.仮説検定により,このコインAが通常のコインと比べて表が出る確率が「違うか・違わないか」を判定したいです.
このとき,まず2つの仮説を設定するのでした.
- H0:表が出る確率は1/2である
- H1:表が出る確率は1/2ではない
そしてH0が成り立っている仮定のもとで,論理展開していきます.
表が出る確率が1/2のコインを20回投げると,表が出る回数の分布は図のようになります
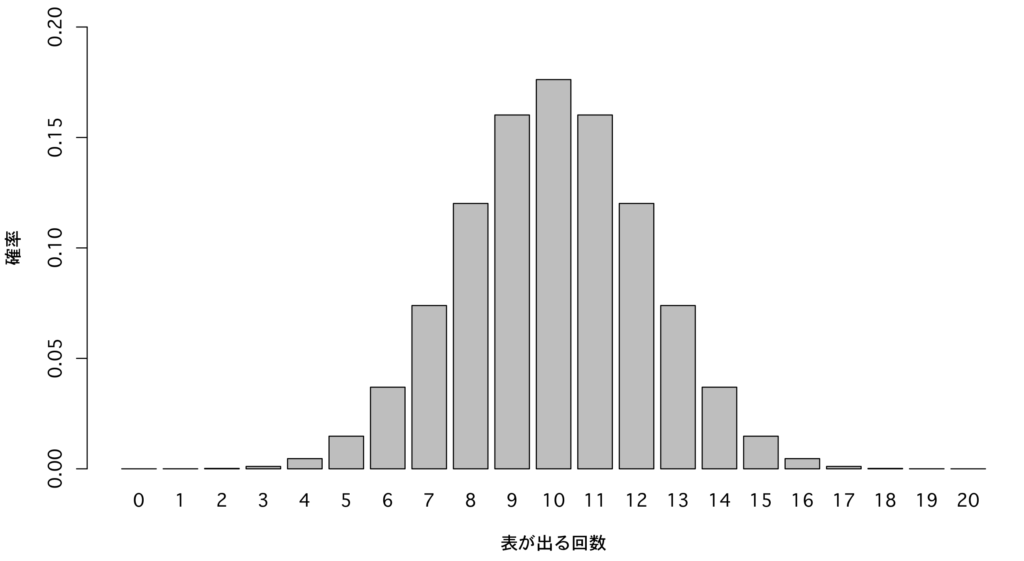
ここで,実際に得られた値かそれ以上に極端に差があるデータが得られる確率(=P値)を評価すると,
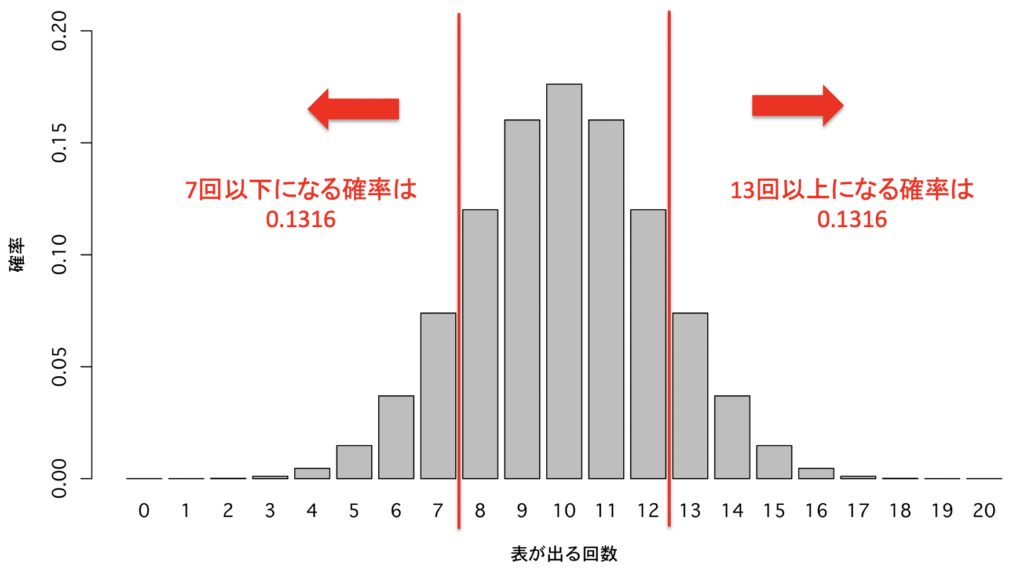
P値 = 0.1316 + 0.1316 = 0.2632となります.
P > 0.05ですので,H0の仮定を棄却することができず,「違うか・違わないか」の判定を保留するのでした.
- (補足)これは「表 / 裏」の二値変数で,1グループ(1変数)に対する検定ですので,母比率の検定(=1標本カイ二乗検定)などと呼ばれたりしています.入門③で頻用する検定の一覧表を載せています.
αエラーについて
ちなみに,5回以下または15回以上表が出るとP<0.05になり,統計的有意差が得られることになります.
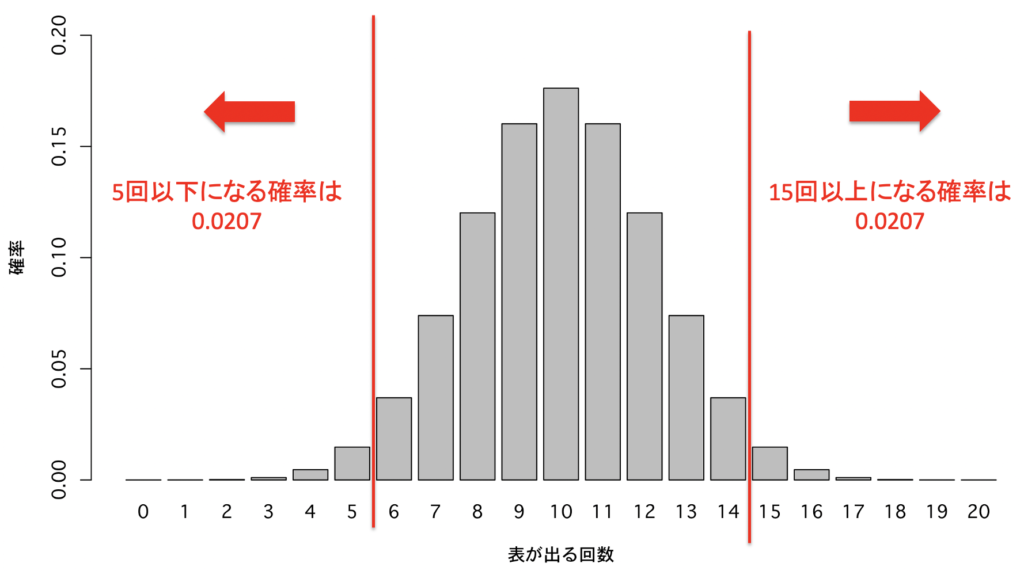
このように,H0が成り立っているのに有意差が出てしまう確率も存在します.有意水準0.05のもとでは,表が出る確率が1/2であるにも関わらず誤って有意差が出てしまう確率は0.05あり,この過誤のことをαエラーと呼びます.
H1を一つの仮説に絞る
ところで,帰無仮説H0 / 対立仮説 H1を前回の入門③でやった「臨床的な差=効果サイズ」で見直してみると
- H0:表が出る確率が50%である
臨床的な差=0 - H1:表が出る確率がXX%である
臨床的な差は0ではない
という状況になっています.つまり表が出る確率が80%の場合,75%の場合,60%の場合,とH1は色々なパターンが無限に考えられるわけです.
この無限に存在するH1を一つの仮説に絞り
- H1:表が出る確率は80%
として考えてみることにしましょう
βエラーと検出力
このH1が成り立っていると仮定したもとで,論理展開してみましょう!表が出る確率が80%のコインを20回投げると,表が出る回数の分布は図のようになります
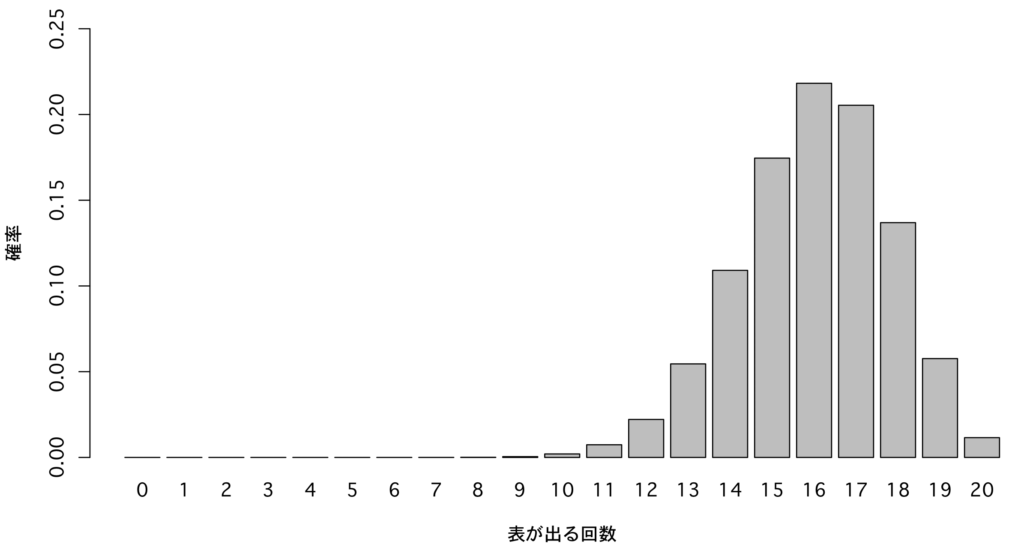
ここで,先ほどの仮説検定の中で有意差あり(P<0.05)となる「5回以下または15回以上表が出る」領域を考えてみると
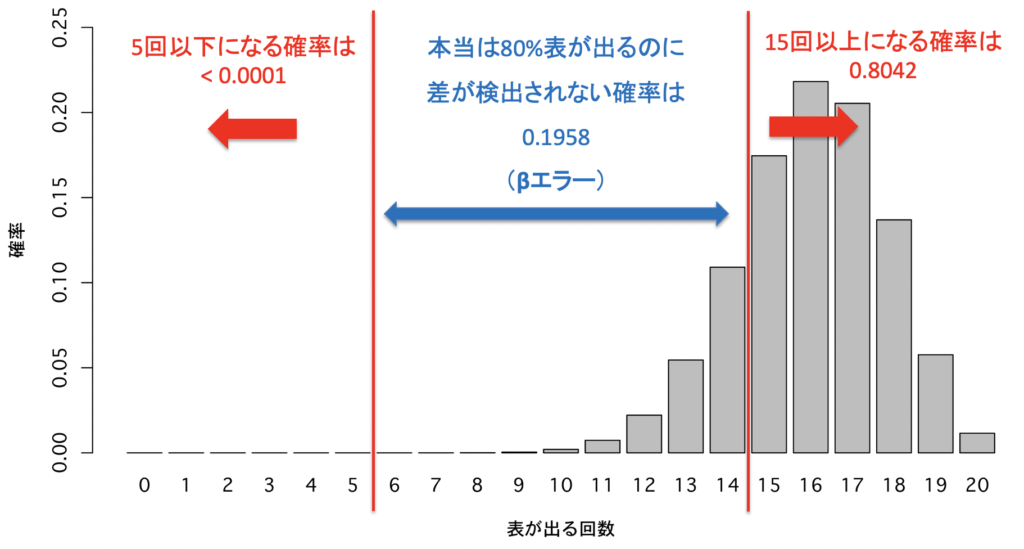
80%表が出るコインが正しく有意差あり,と判定される確率は0.8042です.この「本当は80%表が出るコインAが正しく統計的有意差を出せる確率」のことを検出力といいます.また本当は80%表が出るコインなのに有意差に至らない確率のことをβエラーと呼びます.今回の例ではβエラーは0.1958( = 19.58%)です.
検出力が十分大きい状態の検定ですと,差がある場合に有意差が正しく検出されることになります.今回の例のように7回しか表が出ないデータの場合,「おそらく80%以上の確率で表が出るコインではない」と解釈することが可能になります.
βエラーと検出力は効果サイズとサンプルサイズにより変わる
効果サイズを変える
効果サイズ(=臨床的な差)を変えて
- H1:
表がでる確率は80%→ 表が出る確率は60%
とした場合も考えてみましょう.
表が出る確率が60%のコインを20回投げると,表が出る回数の分布は図のようになります
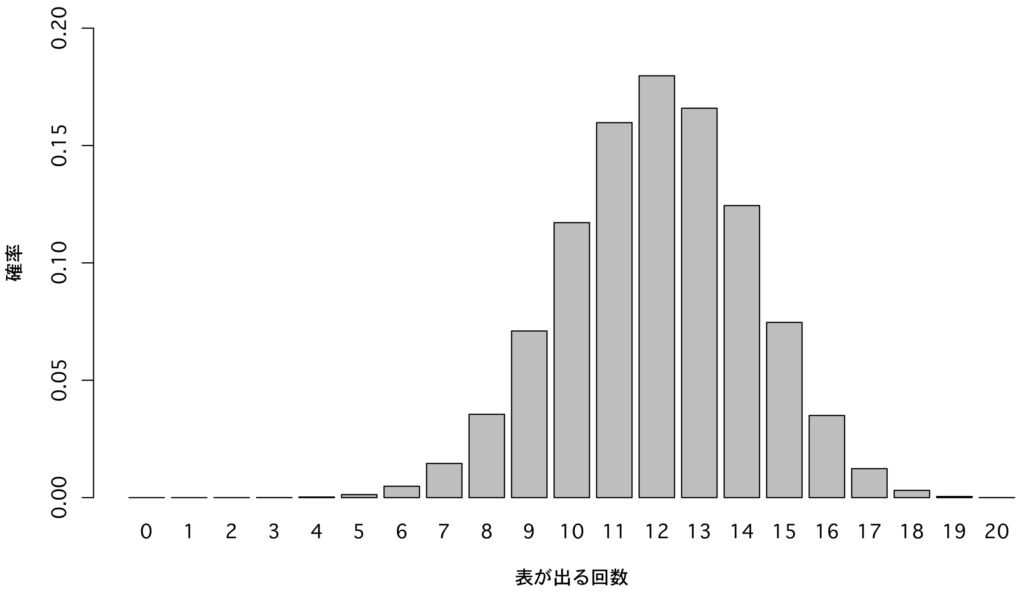
ここで,先ほどの仮説検定の中で有意差あり(P<0.05)となる「5回以下または15回以上表が出る」領域を考えてみると
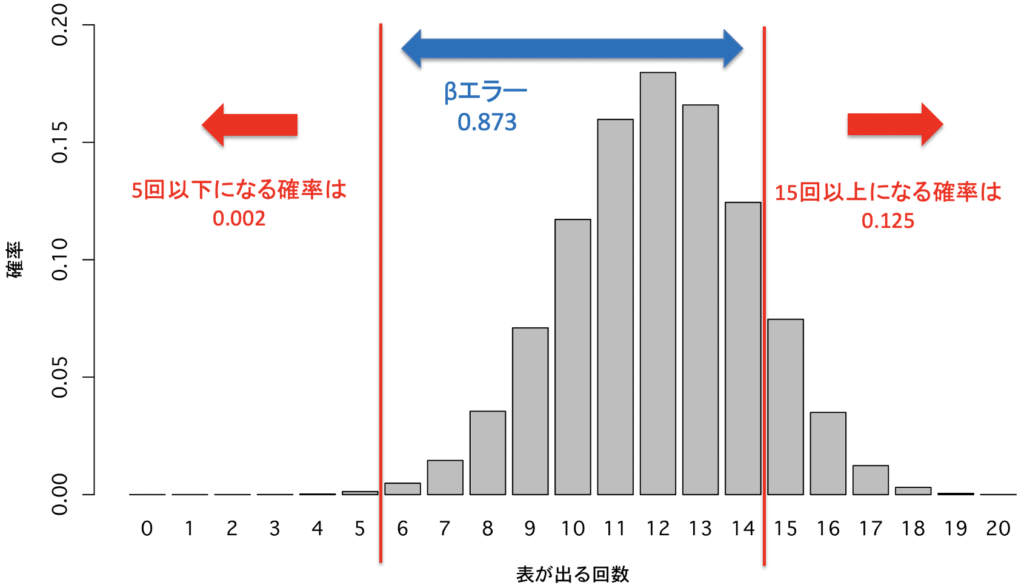
となり,検出力(=正しく有意差が検出される確率)が12.7%しかない状態になります.現状のデータは7回表が出たので,50%の確率で表が出るコインなのか,60%の確率で表が出るコインなのか判別する手がかりは乏しいです.判定を保留する必要があるでしょう.
サンプルサイズを変える
なお,このような場合でもサンプルサイズを増やすことで検出力を大きくすることができます
表が出る確率が50%のコインを200回投げた場合を考えてみると,図のような分布になります.
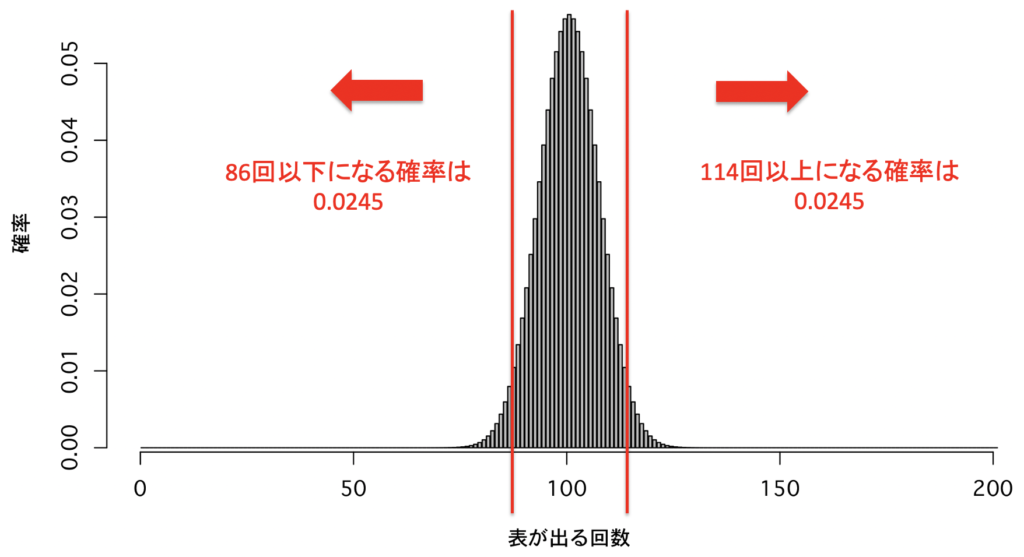
86回以下または114回以上表が出るとP<0.05になり,統計的有意差が得られることになります.
表が出る確率が60%のコインを200回投げた場合を考えてみると,図のような分布になります.
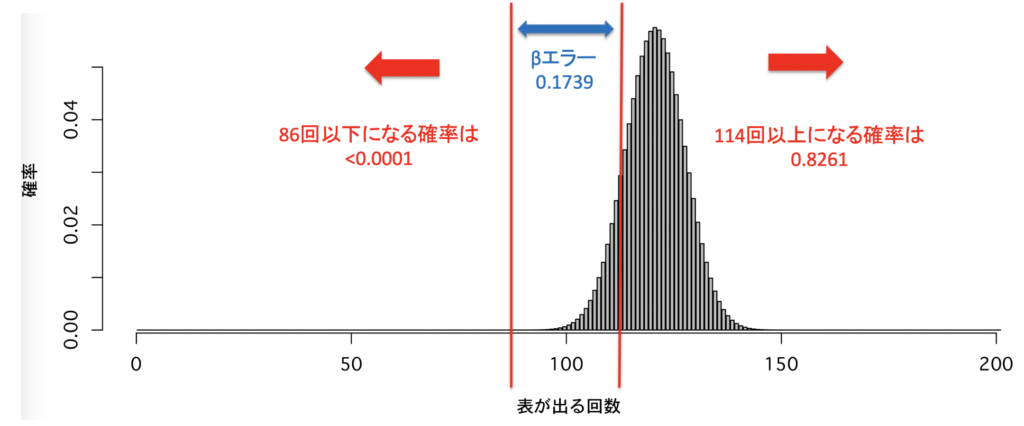
検出力(=正しく有意差が検出される確率)が82.61%となりました.よって有意差が得られない領域に入った場合,「おそらく60%以上の確率で表が出るコインではない」と解釈することが可能になります.
αエラーとβエラーのまとめ
少し説明が複雑になってきましたので,表にしてまとめましょう!

- αエラー:帰無仮説が真であるにも関わらず,統計的有意な結果を得て,帰無仮説を棄却する確率
- βエラー:対立仮説が真であるにも関わらず,統計的有意でない結果を得る確率
- 検出力:対立仮説が真であるときに,統計的有意な結果を得て,正しく対立仮説を採択できる確率.\(1-\beta\)と一致.
- 有意水準5%のもとではαエラーは常に5%
- βエラーと検出力は臨床的な差(=効果サイズ)とサンプルサイズによって変わる
サンプルサイズ設計
通常の検定では,βに関する評価は野放しになっている状態です.そのため,有意差があったときのみ評価可能で,有意差がないときは判定を保留することになっていました.
しかし,臨床的な差(=効果サイズ)とサンプルサイズを指定することで,検出力(=\(1-\beta\))を十分大きくすることができれば,有意差がないときの解釈も可能になります.
臨床試験ですと,プロトコル作成の段階で効果サイズを決めて検出力を80%や90%に保つためのサンプルサイズ設計をしてからデータを収集します.このときの効果サイズの決め方のポイントとしましては,「臨床的に意味のある最小の差」を決めることです.そうすることで,有意差が出なかった場合,「臨床的に意味のある差はおそらく無い」と解釈することが可能になります.
一方で,介入のない観察研究ですと効果サイズやβエラーを前もって考慮してデータを集めることはできないので,有意差がないときは判定保留になります.(ちなみに事後検出力の推定,という言葉がありますので,興味のある方は調べてみてください)
ということで検定のお話は無事(?)終了しました.
検定は「差がある / 差がない」の二元論的な意思決定の話ばかりでしたが,「結局何%アップするの?」とか「結局血圧は何mmHgくらい違うの?」などの情報を知りたい場合も多いと思います.というわけで次からは統計的推測のもう一つの柱である推定について見ていくことにしましょう.
